Circonférence de la Terre: Ératosthène avait vu (presque) juste

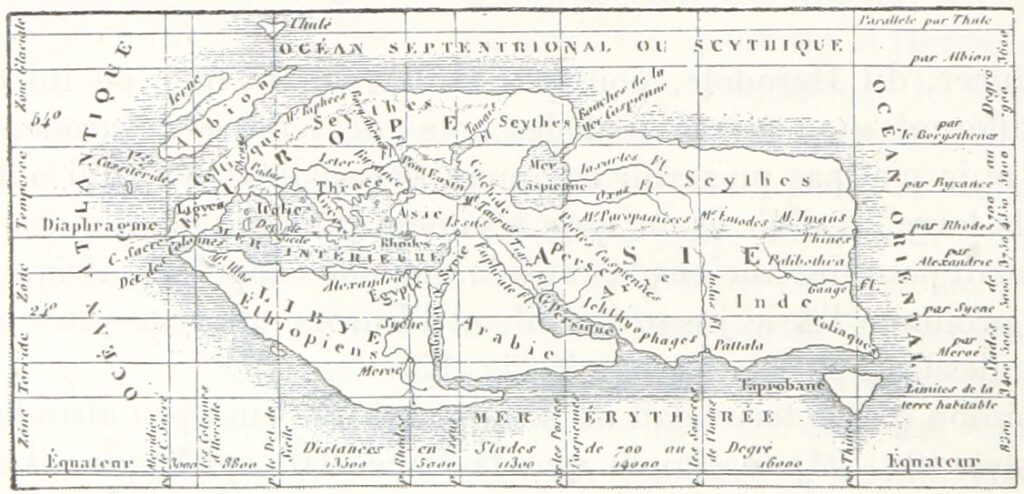
Pour estimer la distance jusqu’aux Indes, Christophe Colomb s’est fié aux calculs de la circonférence de la Terre du savant grec Ptolémée, qui avait lui-même repris ceux du philosophe Posidonius. Sauf qu’ils étaient tous deux à côté de la plaque. Ératosthène, savant et grec lui aussi, avait déjà mieux réussi ce calcul, grâce à un simple bâton et un chameau.

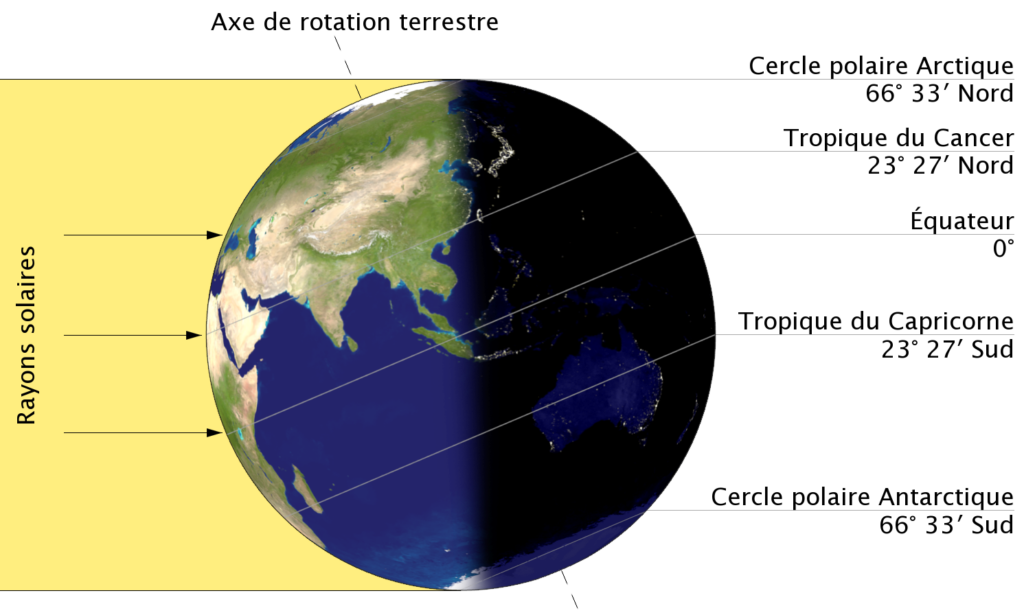
Le philosophe Aristote est l’un des premiers à avoir cherché à mesurer la circonférence de la Terre. En divisant le globe en différentes zones (polaires, tempérées, centrale), il parvient à un chiffre se situant en unités de mesure modernes entre 60 000 et 70 000 km.

Or, la mesure exacte du tour de la Terre est de 40 075 km. On peut pardonner ce léger écart à Aristote. Le GPS n’existait pas encore.

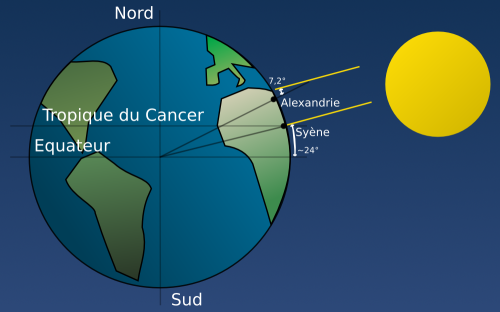
Quant à Posidonius, il errera dans l’autre sens. En observant l’étoile Canopus à Rhodes puis à Alexandrie, en Égypte, ce philosophe, astronome et géographe pense avoir déterminé l’angle – ou la fraction du cercle – qui sépare les deux endroits.

Il mesure ainsi une circonférence de 18 000 km, soit moins de la moitié de la distance que l’on connait aujourd’hui.

Ératosthène, un génie à Alexandrie

Né en 276 av. J.-C., Ératosthène est appelé à Alexandrie par le pharaon Ptolémée III (à ne pas confondre avec le savant). Le souverain souhaite que le savant veille à l’éducation de son fils, le futur Ptolémée IV.

Une vingtaine d’années plus tard, le pharaon nomme Ératosthène directeur de la célèbre bibliothèque d’Alexandrie, créée par le fondateur de la dynastie lagide, Ptolémée Ier.

Dans ce temple de la connaissance, Ératosthène peut mener de multiples recherches dans des domaines variés, que ce soit l’altitude des montagnes, le catalogage des étoiles, la répartition des continents ou encore l’invention d’un procédé mathématique pour trouver les nombres premiers.

C’est déjà un bon bagage. Mais Ératosthène passera plutôt à l’Histoire pour son calcul de la circonférence de la Terre. On pourrait dire que sa méthode était simple et qu’il fallait seulement y penser. À bien y regarder… pas si simple que ça.

Peut-être a-t-il été inspiré par la personne d’Archimède, l’un des plus grands mathématiciens de l’Antiquité, qu’il a côtoyé lors du séjour de celui-ci à Alexandrie.

Au bon moment, au bon endroit

Il faut dire qu’Ératosthène vivait dans l’endroit idéal pour faire ce genre de calculs. Il lui fallait d’abord deux lieux situés sur un même méridien (ou à peu près), dont l’un devait être près du tropique du Cancer.

Or, la ville de Syène (aujourd’hui Assouan, dans le sud de l’Égypte) se trouve un peu au-dessus de ce tropique, qui revêt une importance cruciale dans cette expérience. Pourquoi? C’est qu’au solstice d’été, le Soleil frappe directement le tropique du Cancer. Ce jour-là, l’astre lumineux ne produit aucune ombre, car il est à la verticale de ce tropique à midi.

Ératosthène avait constaté (ou on lui avait dit) qu’au solstice d’été, à Syène, le Soleil se reflétait parfaitement au fond d’un puits vertical. Il savait également qu’au même moment, à Alexandrie, on pouvait apercevoir une petite ombre au fond d’un puits, car la ville était plus au nord du tropique.

L’angle de l’ombre au solstice d’été

Le savant a l’idée de génie de calculer l’angle que fait cette ombre sur le sol le jour du solstice d’été à Alexandrie. Il y plante donc un bâton, qui était en fait un gnomon, soit un piquet utilisé à l’époque pour les cadrans solaires.

Il part évidemment du principe que la Terre est ronde, ce qu’avaient déjà attesté les savants grecs longtemps auparavant, et que le Soleil est très éloigné, ce qui fait en sorte que ses rayons vont sembler atteindre la planète comme un faisceau parallèle.

Ces prémices sont la clé du calcul qu’Ératosthène veut établir. Par déduction géométrique, l’angle de l’ombre projetée sur le sol d’Alexandrie par le bâton correspond à l’angle que formerait une ligne qui partirait du centre de la Terre vers le bâton avec une autre vers Assouan.

La fraction du cercle représentée par l’angle de l’ombre à Alexandrie est la même que celle entre les deux villes par rapport à la circonférence de la Terre, car celles-ci sont sur la même longitude.

Ératosthène mesure ainsi un angle de 7,2 degrés, exactement un cinquantième de 360 degrés, soit un cercle. Ou un méridien. C’était un véritable coup de chance, car il lui suffit maintenant de multiplier la distance entre Alexandrie et Syène simplement par 50 pour obtenir la mesure du cercle de la planète.

Oui, mais c’est quoi la distance?

Ératosthène doit maintenant trouver un moyen de mesurer la distance entre les deux villes.

La méthode employée fait l’objet de débats, mais on rapporte le plus souvent qu’Ératosthène a eu recours à des chameaux, réputés pour avoir un pas très régulier. Certaines sources affirment qu’il s’agissait en fait de dromadaires.

D’autres avancent que ce sont plutôt des bématistes qui ont fait le calcul. Les bématistes étaient des arpenteurs très sollicités qui pouvaient mesurer assez précisément les distances en comptant le nombre de pas.

Quel que soit le moyen utilisé, on arrive à une distance Syène-Alexandrie de 5000 stades. En multipliant par 50, on arrive à une circonférence terrestre de 250 000 stades.

Maintenant, la question qui tue: à quoi correspond un stade dans nos mesures modernes?

Bien que le stade était une unité de mesure répandue dans l’ensemble de l’empire fondé par Alexandre le Grand, sa valeur pouvait varier d’un endroit à l’autre. Pierre-Simon Girard, un ingénieur qui participe à la campagne d’Égypte de Bonaparte, a estimé qu’un stade égyptien – région où Ératosthène a fait ses mesures – mesurait environ 158 mètres.

Deux erreurs qui s’annulent

Faisons maintenant le calcul final: un stade fait 158 mètres qui, multipliés par 250 000 stades (évaluation d’Ératosthène), donnent 39 500 km, soit 575 km de moins que la distance exacte, qui est, rappelons-le, de 40 075 km.

Le savant est presque arrivé pile, même s’il a commis deux erreurs: les deux villes ne sont pas exactement sur le même méridien, et la distance entre les deux est de 5 346 stades et non 5 000. Mais par un hasard étonnant, ces deux erreurs se sont annulées.

La marge d’erreur d’Ératosthène était donc de moins de 2%. Tout ça grâce à un bâton, des chameaux – ou dromadaires (peut-être) –, beaucoup de jugeote et… un peu de chance.